Tree Clustering 이후에는 Quasi-Diagonalization이라는 과정을 거친다.
Quasi-Diagonalization을 직역하자면 준대각화, 혹은 유사대각화라고 할 수 있겠는데, Quasi-가 ‘준-‘ 혹은 ‘유사-‘라는 뜻을 갖고 있기 때문이다.
실제로 상관계수행렬은 대각선을 따라 정렬된다.
높은 상관계수일수록 대각선과 가까운 곳에, 낮은 상관계수일수록 대각선과 낮은 곳에 위치한다.
상관계수가 큰 asset들일수록 list에서 가까운 곳에 위치하기 때문이다.
아래 그림을 통해 Quasi-Diagonalization의 효과를 직관적으로 이해할 수 있을 것이다.

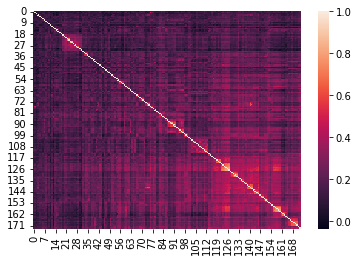
Quasi-Diagonalization 단계에서는 asset의 위치를 재조정하고, 유사한 asset들이 list에서 가까운 자리에 위치하게 한다. 이를 통해 Recursive Bisection 단계를 원활히 수행할 수 있고, n차원 상의 Euclidean Distance를 1차원 list로써 나타낼 수 있다.
이를 위해서 다음과 같은 코드가 사용된다.
def getQuasiDiag(link):
# Sort clustered items by distance
link=link.astype(int)
sortIx=pd.Series([link[-1,0],link[-1,1]])
numItems=link[-1,3] # number of original items
while sortIx.max()>=numItems:
sortIx.index=range(0,sortIx.shape[0]*2,2) # make space
df0=sortIx[sortIx>=numItems] # find clusters
i=df0.index;j=df0.values-numItems
sortIx[i]=link[j,0] # item 1
df0=pd.Series(link[j,1],index=i+1)
sortIx=sortIx.append(df0) # item 2
sortIx=sortIx.sort_index() # re-sort
sortIx.index=range(sortIx.shape[0]) # re-index
return sortIx.tolist()
하지만 이를 직관적으로 이해하기는 힘들 것이다. Linkage matrix에 대한 이해가 먼저 필요하기 때문이다.
[link: Linkage Matrix]
그러므로 아래 예시를 통해 차근차근 알고리즘을 이해해보자.
다음과 같은 11개의 종목
- 삼성전자 … 0
- 하이닉스 … 1
- 카카오 … 2
- 네이버 … 3
- LG유플러스 … 4
- 현대자동차 … 5
- 포스코 … 6
- 대우건설 … 7
- 기아자동차 … 8
- 삼성전자 우선주 … 9
- KT … 10
으로 구성된 포트폴리오 리스트를 Quasi-Diagonalization을 통해 재배열할 것이다.
처음에는 linkage matrix를 받아오는 것으로 시작한다. Tree Clustering을 통해 얻은 linkage matrix를 불러온다.
형태는 다음과 같다고 가정하자. (임의의 값이다. 근거는 없다.)
#Linkage matrix Example
“””
[11[ 0, 9, 0.2, 2],
12 [ 5, 8, 0.24, 2],
13 [ 4, 10, 0.3, 2],
14 [ 2, 3, 0.31, 2],
15 [ 1, 11, 0.45, 3],
16 [ 6, 7, 0.56, 2],
17 [ 14, 15, 0.72, 5],
18 [ 13, 17, 0.88, 7],
19 [ 12, 16, 0.91, 4],
20 [ 18, 19, 1.12, 11]]
“””
그 다음엔 재배열된 assets(과 link)들이 위치할 list를 만들자. 논문에서는 sortIx라는 pandas Series를 정의하는 부분이다.
# sortIx = [ ]
여기에 맨 마지막 link의 두 원소를 넣자.
# sortIx = [18, 19]
이후 sortIx 안의 link들을 link가 가리키는 원소들로 대체하자.
18은 13과 17, 19는 12와 16을 가리키므로, sortIx는 다음과 같다.
# sortIx = [13, 17, 12, 16]
이 과정을 sortIx에 모든 link가 없어질 때까지 반복한다.
# sortIx = [4, 10, 14, 15, 5, 8, 6, 7]
sortIx 안의 원소의 위치는 정렬이 끝날 때까지 바뀌지 않는다.
이로 인해 Euclid Distance가 가까운 asset들은 sortIx에서도 가까운 곳에,
Euclid Distance가 먼 asset들은 sortIx에서도 상대적으로 떨어진 곳에 위치하게 된다.
# sortIx = [4, 10, 2, 3, 1, 11, 5, 8, 6, 7]
최종 결과는 아래와 같다.
# sortIx = [4, 10, 2, 3, 1, 0, 9, 5, 8. 6, 7]
이를 다시 list로 표시하면 아래와 같다.
- LG유플러스
- KT
- 카카오
- 네이버
- 하이닉스
- 삼성전자
- 삼성전자 우선주
- 현대자동차
- 기아자동차
- 포스코
- 대우건설
보다시피 거리가 가까운 asset들( 하닉-삼전-삼전우, 현-기, lg-kt 등)이 더욱 가까운 곳에 위치하는 것을 알 수 있다.
